Pertidaksamaan Nilai Mutlak

Nilai mutlak suatu bilangan real x merupakan jarak antara bilangan itu dengan nol pada garis bilangan. Dan dilambangkan dengan │x│. Secara formal nilai mutlak didefinisikan:

Contoh : │–3│ = 3 , │5│ = 5 , │4 – 6│ = │4 – 6│
Sifat-sifat pertidaksamaan nilai mutlak pada interval terbuka:

Sifat-sifat diatas berlaku pula untuk interval tertutup.

Untuk pemahaman lebih lanjut, ikutilah pola soal beriku ini:

01. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) │x – 6│ ≤ 9
(b) │x + 2│ > 4
Jawab
(a) │x – 6│ ≤ 9
      –9 ≤ x – 6 ≤ 9
      –9 + 6 ≤ x – 6 + 6 ≤ 9 + 6
      –3 ≤ x ≤ 15
(b) │x + 2│ > 4
      x + 2 < –4 atau x + 2 > 4
      x < –4 – 2 atau x > 4 – 2
      x < –6 atau x > 2

02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) │2x + 1│ ≥ │x – 2│
(b) │x + 2│ > 2│x – 1│
Jawab
(a) │2x + 1│ ≥ │x – 2│
     (2x + 1)2 ≥ (x – 2)²
     4x² + 4x + 1 ≥ x² – 4x + 4
     3x² + 8x – 3 ≥ 0
     (3x – 1)(x + 3) ≥ 0
     x1 = 1/3 dan x2 = –3
     Jadi x ≤ –3 atau x ≥ 1/3

(b) │x + 2│ > 2│x – 1│
      (x + 2)² > 4(x – 1)²
      x² + 4x + 4 > 4(x² – 2x + 1)
      x² + 4x + 4 > 4x² – 8x + 4
      3x² – 12x < 0
      3x(x – 4) < 0
      x1 = 0 dan x2 = 4
     Jadi 0 < x < 4

03. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
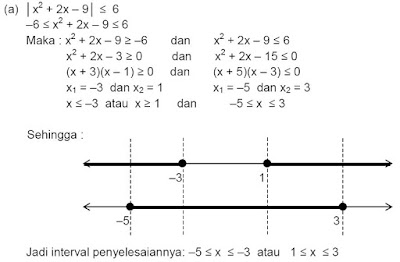
(a) │x² + 2x – 9│ ≤ 6
(b) │x² – 3x – 14│ ≥ 4
Jawab

05. Tentukanlah interval penyelesaian pertidaksamaan │2x + 5│ < x + 4
jawab

Share this post