Pengertian Pertidaksamaan
Notasi pertidaksamaan mencakup :
“ < ” notasi kurang dari
“ > ” notasi lebih dari
“ ≤ ” notasi kurang dari atau sama dengan
“ ≥ ” notasi lebih dari atau sama dengan
Penyelesaian dari suatu pertidaksamaan satu variabel berupa interval atau selang yang sanggup digambarkan dalam suatu garis bilangan
Sedangkan pertidaksamaan linier satu variabel yaitu pertidaksamaan yang memuat satu variabel dengan pangkat tertinggi satu.
Terdapat empat istilah dalam interval, yaitu interval terbuka, interval tertutup, interval berhingga dan interval tak hingga.
Untuk lebih jelasnya ikutilah gambar berikut ini untuk variabel x :
Bentuk lain dari notasi pertidaksamaan yaitu tanda tidak sama dengan (ditulis ≠ ) Namun dalam pembahasan potongan ini, notasi tersebut tidak diuraikan secara mendalam
Sebuah notasi pertidaksamaan sanggup berubah sebab adanya operasi tertentu. Perubahan tersebut sanggup dijelaskan dalam sifat-sifat pertidaksamaan berikut ini :
Sifat-sifat pertidaksamaan :
(1) Tanda/notasi suatu pertidaksamaan tidak berubah bila penambahan atau pengurangan suatu bilangan (variabel) yang sama dilakukan pada kedua ruas pertidaksamaan
Contoh : 3 < 6
3 + 4 < 6 + 4 (kedua ruas ditambahkan 4)
7 < 10
(2) Tanda/notasi suatu pertidaksamaan tidak berubah bila perkalian atau pembagian suatu bilangan (variabel) positip yang sama dilakukan pada kedua ruas pertidaksamaan
Contoh : 3 < 6
3 x 2 < 6 x 2 (kedua ruas dikalikan 2)
6 < 12
(3) Tanda/notasi suatu pertidaksamaan akan berubah bila perkalian atau pembagian suatu bilangan (variabel) negatip yang sama dilakukan pada kedua ruas pertidaksamaan
Contoh : 3 < 6
3 x (–5) < 6 x (–5) (kedua ruas dikalikan –5)
–15 > –30
Untuk lebih jelasnya akan diuraikan dalam referensi soal berikut:
01. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) 3x – 6 < 12 (b) 5x + 3 ≥ 3x – 7
Jawab
(a) 3x – 6 < 12
3x < 12 + 6
3x < 18
x < 6
(b) 5x + 3 ≥ 3x – 7
5x – 3x ≥ –7 – 3
2x ≥ –10
x ≥ –5
02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) 4x – 6 < 9x – 21 (b) 3x – 5 ≥ 7x + 11
Jawab
(a) 4x – 6 < 9x – 21 (b) 3x – 5 ≥ 7x + 11
4x – 9x < 6 – 21 3x – 7x ≥ 5 + 11
–5x < –15 –4x ≥ 16
x > 3 x ≤ –4
03. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) –8 < 3x + 4 < 22 (b) –3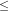
9 – 4x 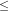29
Jawab
(a) –8 < 3x + 4 < 22
–8 – 4 < 3x + 4 – 4 < 22 – 4
–12 < 3x < 18
–4 < x < 6
(b) –3 ≤ 9 – 4x ≤ 29
–3 – 9 ≤ 9 – 4x – 9 ≤ 29 – 9
–12 ≤ –4x ≤ 20
3 ≥ x ≥ –5
–5 ≤ x ≤ 3
Bentuk Umum pertidaksamaan kuadrat :
ax2 + bx + c < 0
ax2 + bx + c > 0
ax2 + bx + c ≤ 0
ax2 + bx + c ≥ 0
Penyelesaian dari pertidaksamaan tersebut berupa interval berhingga atau interval tak sampai dengan hukum sebagai berikut :
Jika p dan q yaitu akar-akar dari persamaan ax2 + bx + c = 0, maka p dan q merupakan batas-batas interval penyelesaian pertidaksamaan kuadrat tersebut.
Jika D = b2 – 4ac merupakan diskriminannya, maka penyelesaian pertidaksamaan kuadrat sanggup dijelaskan sebagai berikut :
Untuk diskriminan faktual (D > 0), maka akan terdapat dua titik batas interval, yakni p dan q sehingga penyelesaian pertidaksamaan kuadrat sanggup dibantu dengan denah grafik fungsi kuadrat berikut
Untuk diskriminan nol (D = 0), maka akan terdapat satu titik batas interval, misalkan p (p = q) sehingga penyelesaian pertidaksamaan kuadrat sanggup dibantu dengan denah grafik fungsi kuadrat berikut
ax2 + bx + c < 0 penyelesaiannya p < x < p
ax2 + bx + c < 0 penyelesaiannya x < p atau x > p
atau x memenuhi semua bilangan real kecuali p
ax2 + bx + c ≤ 0 penyelesaiannya x ≤ p atau x ≥ p
atau x memenuhi semua bilangan real
ax2 + bx + c > 0 penyelesaiannya p < x < p
atau tidak ada nilai x yang memenuhi
ax2 + bx + c ≥ 0 penyelesaiannya p ≤ x ≤ p
atau x = p
Untuk diskriminan negatif (D < 0), maka tidak terdapat titik batas interval, sehingga penyelesaian pertidaksamaan kuadrat sanggup dibantu dengan denah grafik fungsi kuadrat berikut
ax2 + bx + c < 0 penyelesaiannya tidak ada nilai x yang memenuhi
ax2 + bx + c ≤ 0 penyelesaiannya tidak ada nilai x yang memenuhi
ax2 + bx + c > 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c ≥ 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c < 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c ≤ 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c > 0 penyelesaiannya tidak ada nilai x yang memenuhi
ax2 + bx + c ≥ 0 penyelesaiannya tidak ada nilai x yang memenuhi
Adapun Langkah-langkah penyelesaian pertidaksamaan yaitu sebagai berikut :
(1) Ubah ruas kanan pertidaksamaan menjadi 0
(2) Tentukan batas-batas intervalnya, yaitu akar-akar persamaan kuadratnya
(3) Nyatakan dalam garis bilangan atau gambar grafiknya
(4) Tentukan interval penyelesaiannya
Untuk lebih jelasnya akan diuraikan dalam referensi soal berikut:
01. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) x2 – x – 12 < 0 (b) x2 – 9 ≥ 0
(c) –3x2 + 9x + 30 > 0 (d) 10x – x2 ≤ 24
Jawab
(a) x2 – x – 12 < 0
(x + 3)(x – 4) < 0
x = –3 dan x = 4
–3 < x < 4
(b) x2 – 9 ≥ 0
(x + 3)(x – 3) ≥ 0
x = –3 dan x = 3
x ≤ –3 atau x ≥ 3
(c) –3x2 + 9x + 30 > 0
x2 – 3x – 10 < 0
(x + 2)(x – 5) < 0
x = –2 dan x = 5
–2 < x < 5
(d) x2 – x – 12 < 0
(x + 3)(x – 4) < 0
x1 = –3 dan x2 = 4
–3 < x < 4
02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) x2 – 2x + 8 > 0 (b) 15x – x2 – 18 ≥ x2 + 3x
Jawab
(a) x2 – 2x + 8 > 0
D = (–2)2 – 4(1)(8)
D = –28 < 0
Tidak ada batas interval
Kaprikornus x memenuhi semua bilangan real
(b) 15x – x2 – 18 ≥ x2 + 3x
15x – x2 – 18 – x2 – 3x ≥ 0
–2x2 – 12x – 18 ≥ 0
x2 + 6x + 9 ≤ 0
(x + 3)(x + 3) ≤ 0
x = –3
–3 ≤ x ≤ –3
Atau nilai yang memenuhi hanya untuk x = –3
03. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) x2 – 8x + 16 > 0 (b) x2 + 10x + 25 < 0
Jawab
(a) x2 – 8x + 16 > 0
(x – 4)(x – 4) > 0
x = 4
x < 4 atau x > 4
Atau nilai x memenuhi untuk semua bilangan real kecuali 4
(b) x2 + 10x + 25 < 0
(x + 5)(x + 5) > 0
x = –5
–5 < x < –5
Atau tidak ada nilai x yang memenuhi
4. Sebuah perusahaan sepatu memproduksi dan menjual banyak sekali model sepatu. Untuk satu model sepatu tertentu diperkirakan dijual seharga a rupiah. Jika dalam satu ahad dikeluarkan biaya sebesar M rupiah dan pendapatan yang diterima P rupiah serta dirumuskan M = 2.000.000 – 40.000a dan P = 20.000a – 400a2 maka berapakah batas harga sepatu persatuan harus dijual semoga perusahaan memperoleh laba ?
Jawab
Agar menerima laba maka :
P > M
20000a – 400a2 > 2000000 – 40000a
20000a – 400a2 – 2000000 + 40000a > 0
–400a2 + 60000a – 2000000 > 0
a2 – 150a + 5000 < 0
(a – 100)(a – 50) < 0
Batas interval a1 = 100 dan a2 = 50
Kaprikornus interval harga sepatu yaitu : 50 < a < 100
“ < ” notasi kurang dari
“ > ” notasi lebih dari
“ ≤ ” notasi kurang dari atau sama dengan
“ ≥ ” notasi lebih dari atau sama dengan
Penyelesaian dari suatu pertidaksamaan satu variabel berupa interval atau selang yang sanggup digambarkan dalam suatu garis bilangan
Sedangkan pertidaksamaan linier satu variabel yaitu pertidaksamaan yang memuat satu variabel dengan pangkat tertinggi satu.
Terdapat empat istilah dalam interval, yaitu interval terbuka, interval tertutup, interval berhingga dan interval tak hingga.
Untuk lebih jelasnya ikutilah gambar berikut ini untuk variabel x :
Bentuk lain dari notasi pertidaksamaan yaitu tanda tidak sama dengan (ditulis ≠ ) Namun dalam pembahasan potongan ini, notasi tersebut tidak diuraikan secara mendalam
Sebuah notasi pertidaksamaan sanggup berubah sebab adanya operasi tertentu. Perubahan tersebut sanggup dijelaskan dalam sifat-sifat pertidaksamaan berikut ini :
Sifat-sifat pertidaksamaan :
(1) Tanda/notasi suatu pertidaksamaan tidak berubah bila penambahan atau pengurangan suatu bilangan (variabel) yang sama dilakukan pada kedua ruas pertidaksamaan
Contoh : 3 < 6
3 + 4 < 6 + 4 (kedua ruas ditambahkan 4)
7 < 10
(2) Tanda/notasi suatu pertidaksamaan tidak berubah bila perkalian atau pembagian suatu bilangan (variabel) positip yang sama dilakukan pada kedua ruas pertidaksamaan
Contoh : 3 < 6
3 x 2 < 6 x 2 (kedua ruas dikalikan 2)
6 < 12
(3) Tanda/notasi suatu pertidaksamaan akan berubah bila perkalian atau pembagian suatu bilangan (variabel) negatip yang sama dilakukan pada kedua ruas pertidaksamaan
Contoh : 3 < 6
3 x (–5) < 6 x (–5) (kedua ruas dikalikan –5)
–15 > –30
Untuk lebih jelasnya akan diuraikan dalam referensi soal berikut:
01. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) 3x – 6 < 12 (b) 5x + 3 ≥ 3x – 7
Jawab
(a) 3x – 6 < 12
3x < 12 + 6
3x < 18
x < 6
(b) 5x + 3 ≥ 3x – 7
5x – 3x ≥ –7 – 3
2x ≥ –10
x ≥ –5
02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) 4x – 6 < 9x – 21 (b) 3x – 5 ≥ 7x + 11
Jawab
(a) 4x – 6 < 9x – 21 (b) 3x – 5 ≥ 7x + 11
4x – 9x < 6 – 21 3x – 7x ≥ 5 + 11
–5x < –15 –4x ≥ 16
x > 3 x ≤ –4
03. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) –8 < 3x + 4 < 22 (b) –3
Jawab
(a) –8 < 3x + 4 < 22
–8 – 4 < 3x + 4 – 4 < 22 – 4
–12 < 3x < 18
–4 < x < 6
(b) –3 ≤ 9 – 4x ≤ 29
–3 – 9 ≤ 9 – 4x – 9 ≤ 29 – 9
–12 ≤ –4x ≤ 20
3 ≥ x ≥ –5
–5 ≤ x ≤ 3
Bentuk Umum pertidaksamaan kuadrat :
ax2 + bx + c < 0
ax2 + bx + c > 0
ax2 + bx + c ≤ 0
ax2 + bx + c ≥ 0
Penyelesaian dari pertidaksamaan tersebut berupa interval berhingga atau interval tak sampai dengan hukum sebagai berikut :
Jika p dan q yaitu akar-akar dari persamaan ax2 + bx + c = 0, maka p dan q merupakan batas-batas interval penyelesaian pertidaksamaan kuadrat tersebut.
Jika D = b2 – 4ac merupakan diskriminannya, maka penyelesaian pertidaksamaan kuadrat sanggup dijelaskan sebagai berikut :
Untuk diskriminan faktual (D > 0), maka akan terdapat dua titik batas interval, yakni p dan q sehingga penyelesaian pertidaksamaan kuadrat sanggup dibantu dengan denah grafik fungsi kuadrat berikut
ax2 + bx + c < 0 penyelesaiannya p < x < q
ax2 + bx + c ≤ 0 penyelesaiannya p ≤ x ≤ q
ax2 + bx + c > 0 penyelesaiannya x < p atau x > q
ax2 + bx + c ≥ 0 penyelesaiannya x ≤ p atau x ≥ q
ax2 + bx + c < 0 penyelesaiannya x < p atau x > q
ax2 + bx + c ≤ 0 penyelesaiannya x ≤ p atau x ≥ q
ax2 + bx + c > 0 penyelesaiannya p < x < q
ax2 + bx + c ≥ 0 penyelesaiannya p ≤ x ≤ q
Untuk diskriminan nol (D = 0), maka akan terdapat satu titik batas interval, misalkan p (p = q) sehingga penyelesaian pertidaksamaan kuadrat sanggup dibantu dengan denah grafik fungsi kuadrat berikut
atau tidak ada nilai x yang memenuhi
ax2 + bx + c ≤ 0 penyelesaiannya p ≤ x ≤ p
atau x = p
ax2 + bx + c > 0 penyelesaiannya x < p atau x > p
atau x memenuhi semua bilangan real kecuali p
ax2 + bx + c ≥ 0 penyelesaiannya x ≤ p atau x ≥ p
atau x memenuhi semua bilangan real
ax2 + bx + c < 0 penyelesaiannya x < p atau x > p
atau x memenuhi semua bilangan real kecuali p
ax2 + bx + c ≤ 0 penyelesaiannya x ≤ p atau x ≥ p
atau x memenuhi semua bilangan real
ax2 + bx + c > 0 penyelesaiannya p < x < p
atau tidak ada nilai x yang memenuhi
ax2 + bx + c ≥ 0 penyelesaiannya p ≤ x ≤ p
atau x = p
Untuk diskriminan negatif (D < 0), maka tidak terdapat titik batas interval, sehingga penyelesaian pertidaksamaan kuadrat sanggup dibantu dengan denah grafik fungsi kuadrat berikut
ax2 + bx + c < 0 penyelesaiannya tidak ada nilai x yang memenuhi
ax2 + bx + c ≤ 0 penyelesaiannya tidak ada nilai x yang memenuhi
ax2 + bx + c > 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c ≥ 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c < 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c ≤ 0 penyelesaiannya memenuhi semua bilangan real x
ax2 + bx + c > 0 penyelesaiannya tidak ada nilai x yang memenuhi
ax2 + bx + c ≥ 0 penyelesaiannya tidak ada nilai x yang memenuhi
Adapun Langkah-langkah penyelesaian pertidaksamaan yaitu sebagai berikut :
(1) Ubah ruas kanan pertidaksamaan menjadi 0
(2) Tentukan batas-batas intervalnya, yaitu akar-akar persamaan kuadratnya
(3) Nyatakan dalam garis bilangan atau gambar grafiknya
(4) Tentukan interval penyelesaiannya
Untuk lebih jelasnya akan diuraikan dalam referensi soal berikut:
01. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) x2 – x – 12 < 0 (b) x2 – 9 ≥ 0
(c) –3x2 + 9x + 30 > 0 (d) 10x – x2 ≤ 24
(a) x2 – x – 12 < 0
(x + 3)(x – 4) < 0
x = –3 dan x = 4
–3 < x < 4
(b) x2 – 9 ≥ 0
(x + 3)(x – 3) ≥ 0
x = –3 dan x = 3
x ≤ –3 atau x ≥ 3
(c) –3x2 + 9x + 30 > 0
x2 – 3x – 10 < 0
(x + 2)(x – 5) < 0
x = –2 dan x = 5
–2 < x < 5
(d) x2 – x – 12 < 0
(x + 3)(x – 4) < 0
x1 = –3 dan x2 = 4
–3 < x < 4
02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) x2 – 2x + 8 > 0 (b) 15x – x2 – 18 ≥ x2 + 3x
Jawab
(a) x2 – 2x + 8 > 0
D = (–2)2 – 4(1)(8)
D = –28 < 0
Tidak ada batas interval
Kaprikornus x memenuhi semua bilangan real
(b) 15x – x2 – 18 ≥ x2 + 3x
15x – x2 – 18 – x2 – 3x ≥ 0
–2x2 – 12x – 18 ≥ 0
x2 + 6x + 9 ≤ 0
(x + 3)(x + 3) ≤ 0
x = –3
–3 ≤ x ≤ –3
Atau nilai yang memenuhi hanya untuk x = –3
03. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) x2 – 8x + 16 > 0 (b) x2 + 10x + 25 < 0
Jawab
(a) x2 – 8x + 16 > 0
(x – 4)(x – 4) > 0
x = 4
x < 4 atau x > 4
Atau nilai x memenuhi untuk semua bilangan real kecuali 4
(b) x2 + 10x + 25 < 0
(x + 5)(x + 5) > 0
x = –5
–5 < x < –5
Atau tidak ada nilai x yang memenuhi
4. Sebuah perusahaan sepatu memproduksi dan menjual banyak sekali model sepatu. Untuk satu model sepatu tertentu diperkirakan dijual seharga a rupiah. Jika dalam satu ahad dikeluarkan biaya sebesar M rupiah dan pendapatan yang diterima P rupiah serta dirumuskan M = 2.000.000 – 40.000a dan P = 20.000a – 400a2 maka berapakah batas harga sepatu persatuan harus dijual semoga perusahaan memperoleh laba ?
Jawab
Agar menerima laba maka :
P > M
20000a – 400a2 > 2000000 – 40000a
20000a – 400a2 – 2000000 + 40000a > 0
–400a2 + 60000a – 2000000 > 0
a2 – 150a + 5000 < 0
(a – 100)(a – 50) < 0
Batas interval a1 = 100 dan a2 = 50
Kaprikornus interval harga sepatu yaitu : 50 < a < 100