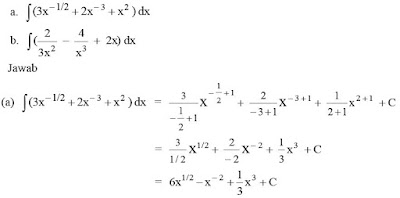Aturan Dasar Integral Fungsi Aljabar
Integral sanggup dipandang sebagai balikan (invers) dari turunan, sehingga integral sering disebut juga sebagai anti turunan.
Sehingga notasi integral ditulis
ʃ f(x) dx = F(x) + c jikalau dan hanya jikalau F’(x) = f(x)
Sebagi contoh:
Jika f(x) = x2 + 6x – 5 maka f ’(x) = 2x + 6
Jika f(x) = x2 + 6x + 10 maka f ’(x) = 2x + 6
Jika f(x) = x2 + 6x – 1/3 maka f ’(x) = 2x + 6
Dari sini diperoleh ʃ 2x + 6 dx = x2 + 6x + C. Konstanta C dianggap mewakili –5, 10, –1/3 dan semua bilangan real yang lainnya.
Dengan berpedoman dari uraian di atas, maka kita sanggup memilih rumus dasar dari pengintegralan, yakni :
Jika y = ax maka y’ = a, untuk a bilangan real.
Jika y' =axn maka y’ = n.axn-1, untuk a dan n bilangan real
Sehingga diperoleh rumusan : jikalau a dan n yaitu bilangan real dengan n ≠ -1, maka :


Sehingga notasi integral ditulis
ʃ f(x) dx = F(x) + c jikalau dan hanya jikalau F’(x) = f(x)
Sebagi contoh:
Jika f(x) = x2 + 6x – 5 maka f ’(x) = 2x + 6
Jika f(x) = x2 + 6x + 10 maka f ’(x) = 2x + 6
Jika f(x) = x2 + 6x – 1/3 maka f ’(x) = 2x + 6
Dari sini diperoleh ʃ 2x + 6 dx = x2 + 6x + C. Konstanta C dianggap mewakili –5, 10, –1/3 dan semua bilangan real yang lainnya.
Dengan berpedoman dari uraian di atas, maka kita sanggup memilih rumus dasar dari pengintegralan, yakni :
Jika y = ax maka y’ = a, untuk a bilangan real.
Jika y' =axn maka y’ = n.axn-1, untuk a dan n bilangan real
Sehingga diperoleh rumusan : jikalau a dan n yaitu bilangan real dengan n ≠ -1, maka :
Untuk pemahaman lebih lanjut, akan diuraikan pada contoh-contoh soal berikut ini :
01. Selesaikanlah integral berikut ini :

02. Selesaikanlah integral berikut ini: